Motivation
- 临床应用中,训练数据与测试数据不匹配,性能急剧下降
- 在部署应用前不可能收集到所有代表性的数据集用于训练模型
提出的框架包含一个在线自适应阶段和一个离线元学习阶段。
本文贡献:
- 提出了一种新颖的在线模型自适应方法,将一个训练好的baseline模型适应于新视频。
- 提出一种元学习方法提升在线优化器。
- 提出用于在密集运动估计任务中训练元学习的实用解决方案。
- 本文方法不限于运动估计任务。
本文采用了与参考文献22类似的self-supervision思想。
通常很难获得真正的心脏运动,因此使用分割蒙版对上述工作进行了定量评估。 在这项工作中,我们也使用这种类型的评估。
Methods
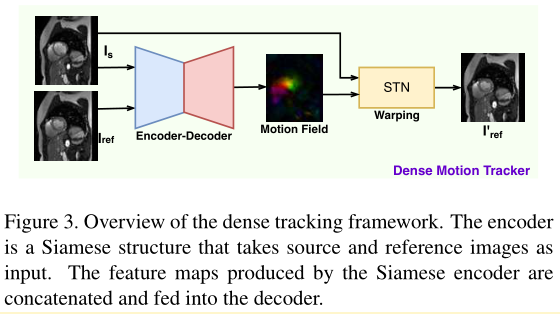
Dense Motion Tracking
整体思想是一种从参考文献22中得到启发的端到端无监督学习方法。
为了进行无监督学习,空间变换器网络[13]用于将源图像变形/扭曲为参考图像,并使用图像重建损失\(L_{mse}\)来最小化扭曲的源图像和参考图像之间的差异。
\(L_{mse}\)是均方误差(MSE);\(L_{smooth}\)是参考文献26中提出的运动域平滑损失,用于避免突然的运动变化;\(L_{con}\)是文献22中提出的双向(前后)流一致性损失。
\[L_{total} = L_{mse} + \alpha_sL_{smooth} + \beta_cL_{con}\]
Online Optimizer
在提出dense tracking的背景下,扩展了tracker以解决数据集分布不匹配的问题。
背后的思想是使给定的tracker能够自动适应新的视频\(x\)。

通过随机梯度下降更新参数,梯度下降步骤是在在线阶段对网络的所有参数执行的。因此,太多的步骤在所有图像对(源和参考)上对它们进行优化在计算上是相当昂贵的。本文目标是仅使用少量的在线样本就可以在少数几个步骤中适应离线模型。通过元学习来优化此过程。(该idea来自MAML【参考文献7】)
Meta-learning
元学习更新策略:
\[\theta \leftarrow \theta-\beta \nabla_{\theta} \frac{1}{N} \sum_{i}^{N} L_{i}\left(f_{\theta_{i}^{\prime}}\right)\]

Practical Version of the Meta-Learning
Memory limitation and solution
Dense motion tracker需要较大尺寸的图像,元学习的优化器需要计算与特定视频相关联的每个独立模型的导数。未解决这个问题,通过利用等式中的梯度算子和平均算子是可交换的性质,交换两个运算符,如下所示:
\[\nabla_{\theta} \frac{1}{N} \sum_{i}^{N} L_{i}\left(f_{\theta_{i}^{\prime}}\right) \Leftrightarrow \frac{1}{N} \sum_{i}^{N} \nabla_{\theta} L_{i}\left(f_{\theta_{i}^{\prime}}\right)\]
First order derivative approximation
上式中需要二阶导数,涉及到计算二阶Hessian矩阵,这在计算上是昂贵的。作为解决方法,本文使用一阶近似,其有效性在MAML中得到了证明[7]。
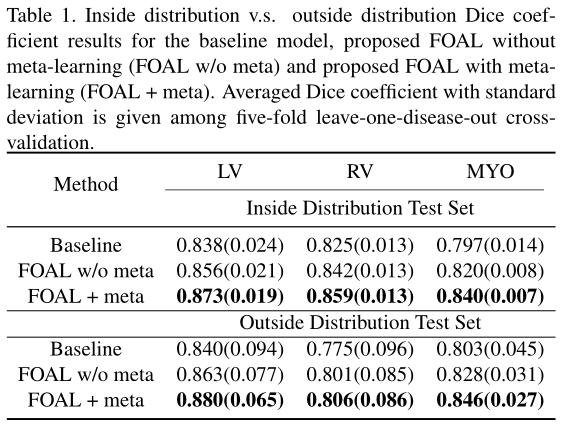
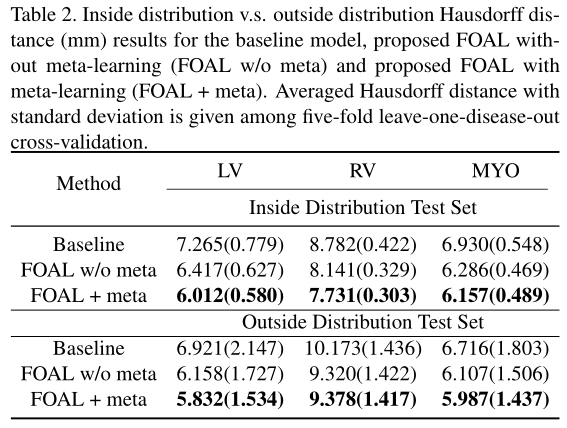
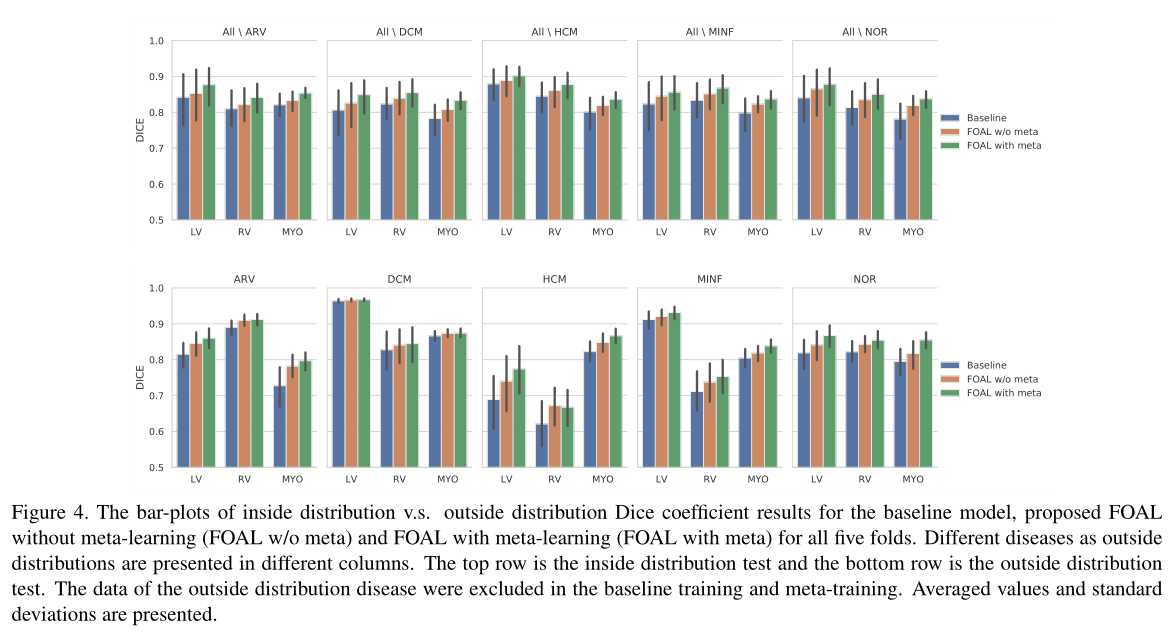
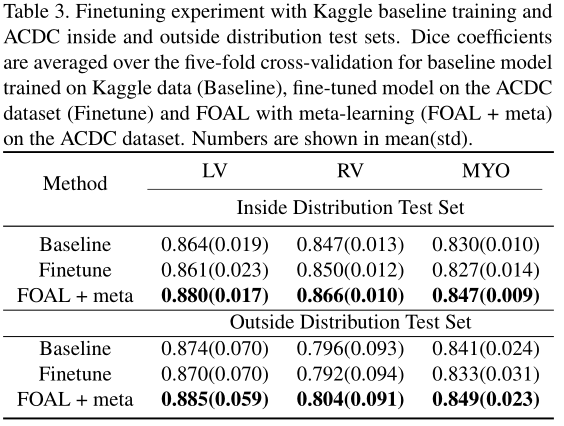
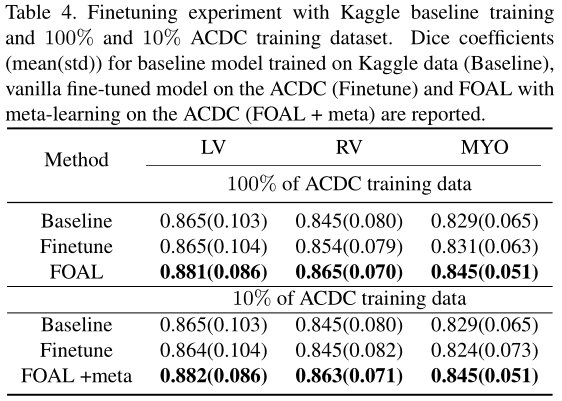
Experiments