Code: https://github.com/msahasrabudhe/miccai2020_self_sup_nuclei_seg
Motivation
针对医疗图像标注困难,提出了一种基于自监督的组织病理学图像细胞核分割方法。
本文贡献
- 基于核是该任务的判别特征的前提下,使用尺度分类作为自监督信号。
- 采用基于Dilated的全卷积网络生成分割图作为注意力Map
- 引入正则化约束以生成语义上有意义的分割结果
Methods
主要思想是,给定一张WSI贴片,以一定放大倍数观察,可以通过观察贴片中核的大小和纹理确定放大水平。基于此,假设原子核足以确定放大倍数,并且其他图像不是必需的。
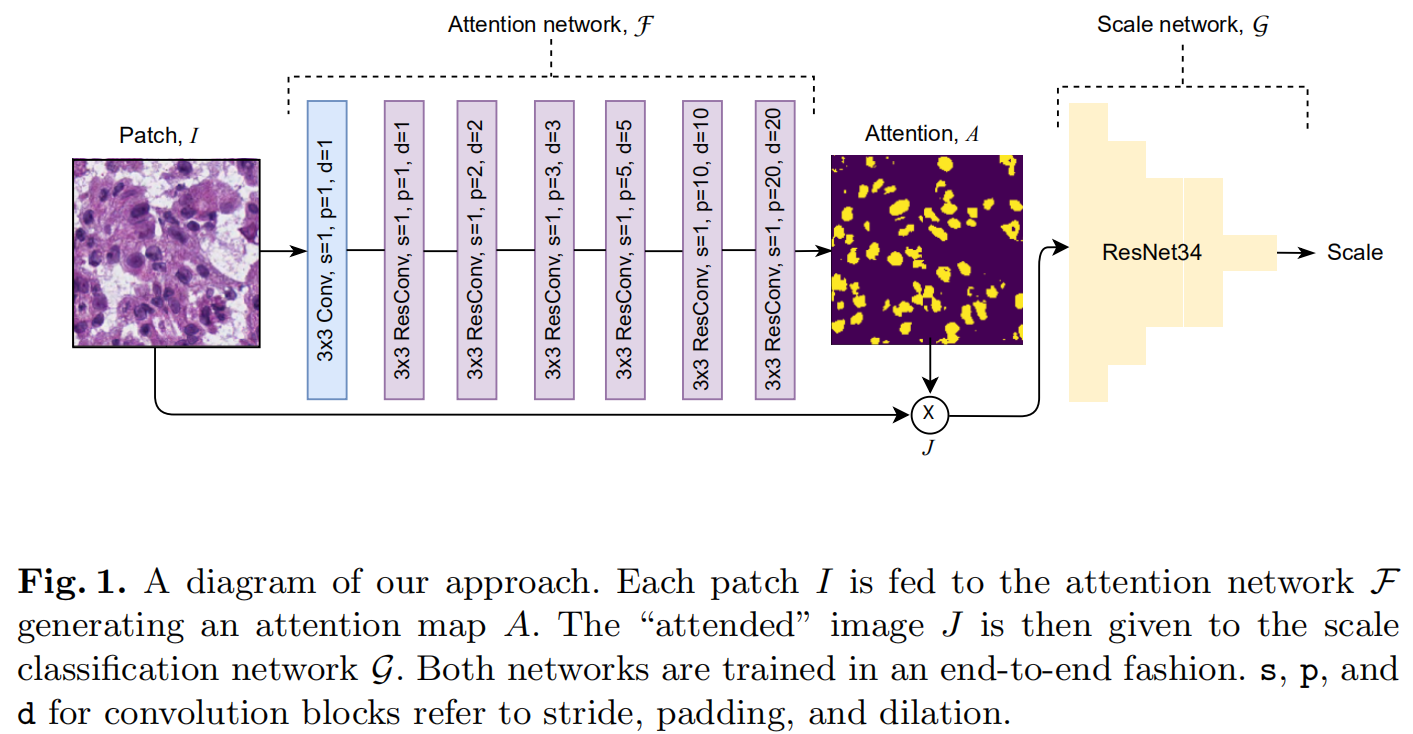
假设学习了一个对scale敏感的网络,专门用于区分特征的正确比例。给定一组WSIs,以固定的放大倍数\(C\)提取所有组织patches。首先,通过Attention network学习一个二分类的分割图\(A \in [0, 1]^{1\times H \times W}\)。输入图像与注意力图相乘可以确定放大比例\(A \odot I\)。
confidence map表示为\(A=\sigma(a)\),\(a=F(I) \in \mathbb{R}^{1\times H \times W}\),\(\sigma(\cdot)\)为sigmoid函数。通过应用稀疏性正则化,迫使注意力图只关注input patch的局部。 \[
\tau=\frac{1}{B} \sum_{b=1}^{B} \mathbf{a}_{b}^{(\eta)}
\] \(J=A \odot I\)表示缩放比例,通过负对数似然法来训练分类网络G,然后训练注意力网络\(F\) \[
\mathcal{L}_{\text {scale }}(\hat{\mathbf{p}}, l)=-\log \hat{p}_{l} ; \hat{p}_{i}=[\operatorname{softmax}(\hat{\mathbf{s}})]_{i} ; \hat{\mathbf{s}}=\mathcal{G}(J) ; 1 \leq i \leq N_{\mathcal{C}}
\]
Smoothness Regularization
希望\(A\)在语义上有意义且平滑,要关注核而不是高频区域,在注意力图上加入了平滑度正则化。 \[ \mathcal{L}_{\mathrm{smooth}}=\frac{1}{(H-1)(W-1)} \sum_{i, j}\left\|A_{i+1, j}-A_{i, j}\right\|_{1}+\left\|A_{i, j+1}-A_{i, j}\right\|_{1} \]
Transformation Equivariance
加入语义一致性的常用约束 \[ \mathcal{L}_{\mathrm{equiv}}=\frac{1}{H W}\|\sigma(t(\mathcal{F}(I)))-\sigma(\mathcal{F}(t(I)))\|_{2}^{2} \] 总的损失为三者相加,其中\(\mathcal{L}_{scale}\)为自监督loss \[ \mathcal{L}_{total} = \mathcal{L}_{scale}+\mathcal{L}_{smooth}+\mathcal{L}_{equiv} \]
Post Processing, Validation, and Model Selection
通过三步后处理得到最终结果:
- 使用开和闭的形态学操作
- 应用高斯模糊
- 使用分水岭算法得到最终结果
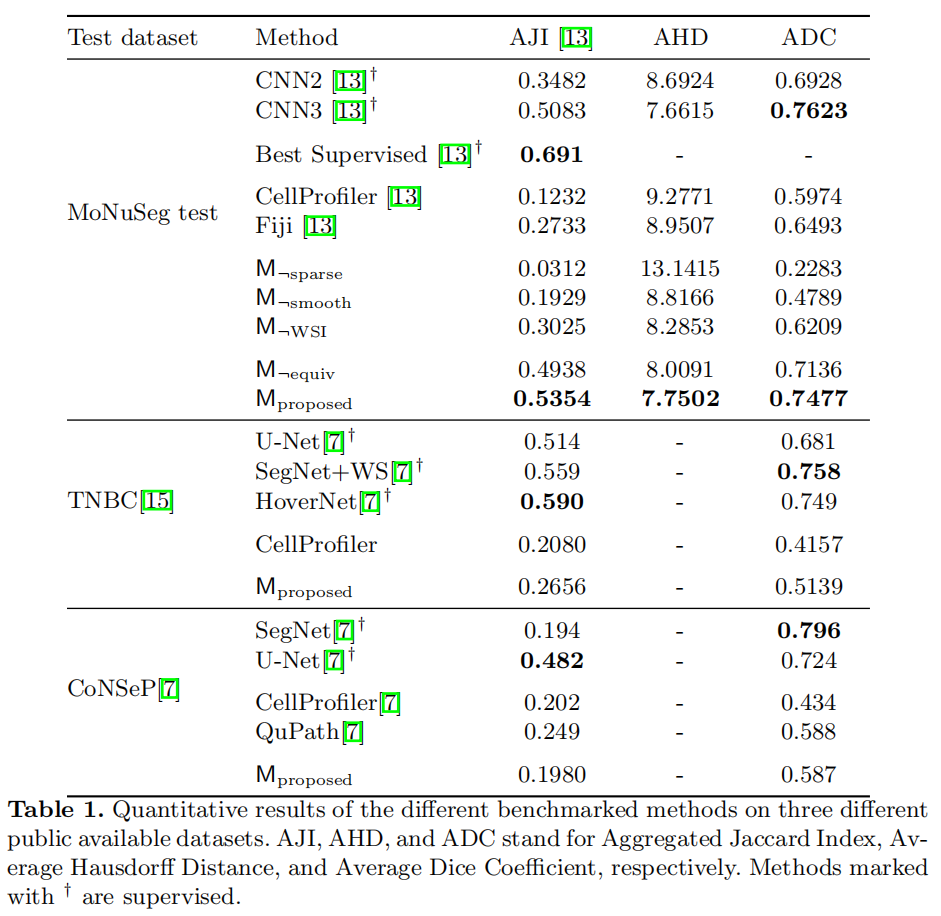
Experiments