Motivation
- 提出一种新颖的弱监督方法,用于图像中角膜和虹膜的分割
- 从弱标签样本中提取信息外,添加微观模型用于指导宏观模型
- 除了从完全注释图像中学习逐像素注释信息外,宏观微观流还旨在为训练模型提供更多高级语义信息
- 引入不确定性策略,以获得更准确和更稳定的指导
Methods
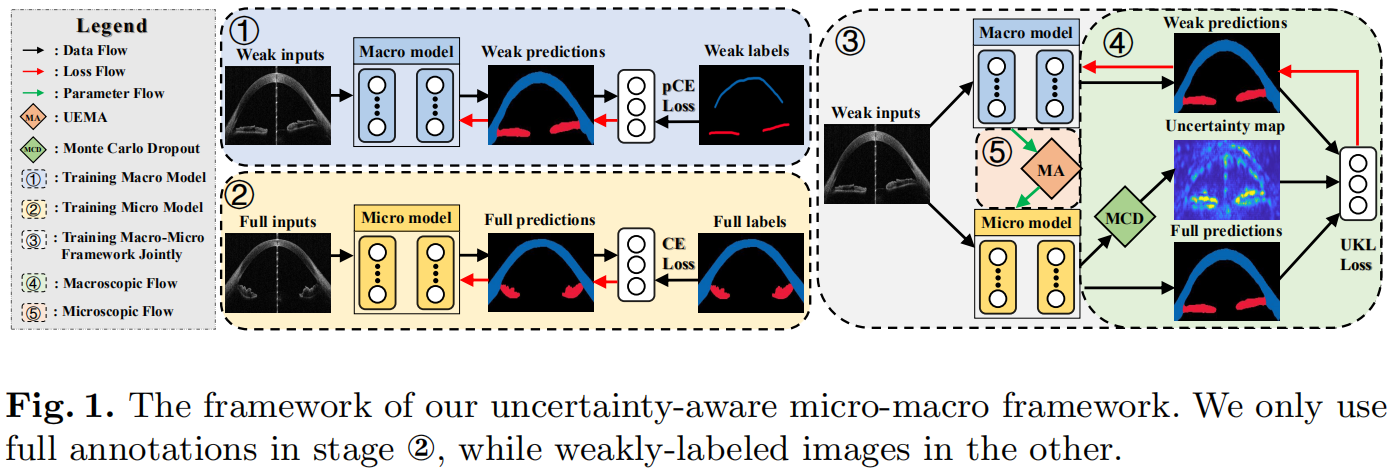
该框架由宏观模型和微观模型两部分组成。完全标注数据为每一个像素点的人工标签,弱标签数据为通过圆圈、点、涂鸦等标注出感兴趣的区域。
分为两个阶段进行优化:
- 使用完全标注的数据和弱标签数据分别训练微观模型和宏观模型
- 将两个模型联合训练,这个阶段只使用弱标签数据,两个模型相互提供指导,以实现更好的分割效果
Loss Functions for the Macro and Micro Model
第一阶段,使用弱标签数据训练宏观模型,使用完全标注数据训练微观模型。
训练损失分别为: \[ \mathcal{L}_{\text {micro}}\left(x_{i}\right)=-\frac{1}{K \times C} \sum_{k=1}^{K} \sum_{c=1}^{C} y_{i}^{s}(k, c) \log m_{i}^{s}(k, c) \]
\[ \mathcal{L}_{\text {macro}}\left(x_{j}\right)=-\frac{1}{\sum_{k=1}^{K} s_{j}(k) \times C} \sum_{k=1}^{K} \sum_{c=1}^{C} s_{j}(k) \cdot y_{j}^{w}(k, c) \log m_{j}^{w}(k, c) \]
Uncertainty-aware KL Loss for the Macroscopic Flow
两个模型的输出之间采用KL散度损失来微调宏观模型,并引入不确定性图来选取可靠的像素点用于指导。因为可以将蒙特卡洛样本的方差视为不确定性的近似值,所以可以将微观模型的不确定性图\(U\)表示为: \[ \mu_c = \frac{1}{T}\sum_{t=1}^{T}{p_t^c} \quad and \quad U=\frac{1}{T \times C}\sum_{t=1}^{T}\sum_{c=1}^{C}(p_t^c-\mu_c)^2 \] 因此可以得到不确定性图指导的KL损失: \[ \begin{aligned} \mathcal{L}_{U K L} &=\frac{\mathbb{I}(U<\tau) \cdot \mathcal{L}_{K L}\left(m_{j}^{w} \| m_{i}^{s}\right)}{\sum \mathbb{I}(U<\tau)} \\ &=\frac{1}{\sum_{k=1}^{K} \mathbb{I}(U(k)<\tau) \times C} \sum_{k=1}^{K} \sum_{c=1}^{C} \mathbb{I}(U(k)<\tau) \cdot m_{j}^{w}(k, c) \log \left(\frac{m_{j}^{w}(k, c)}{m_{i}^{s}(k, c)}\right) \end{aligned} \]
Uncertainty-aware EMA as the Microscopic Flow
本文使用宏观模型学习得到的分割结果为微观模型提供线索,提出一个不确定性指数移动平均机制(uncertainty-aware exponential moving average, UEMS)用于联合训练 \[ \theta^{s}=\alpha \theta^{s}+(1-\alpha) \theta^{w} \quad \text { and } \quad \alpha=\frac{\sum_{k=1}^{K} \mathbb{I}(U(k)<\tau)}{\sum_{k=1}^{K} \mathbb{1}} \]
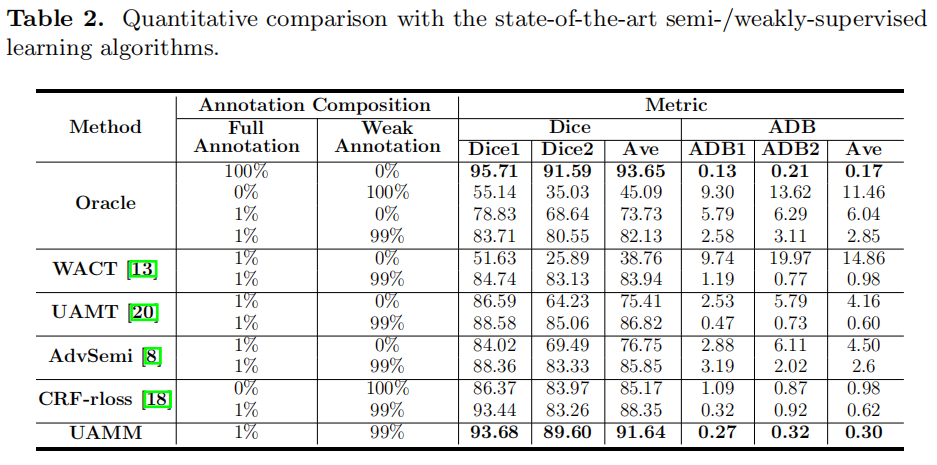
Experiments