Motivation
- 注释医学图像需要有经验的医生花费数小时或数天进行研究,不仅费力而且十分昂贵
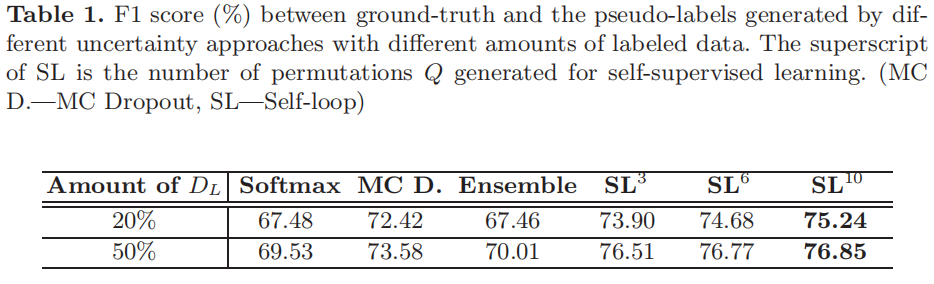
- 使用未标记数据的伪标签(通过不确定性估计由分割算法自动生成)是潜在的解决方案之一,其中最受欢迎的方法是:
- softmax概率图
- 蒙特卡洛drop
- 网络结构中的不确定性估计
Methods
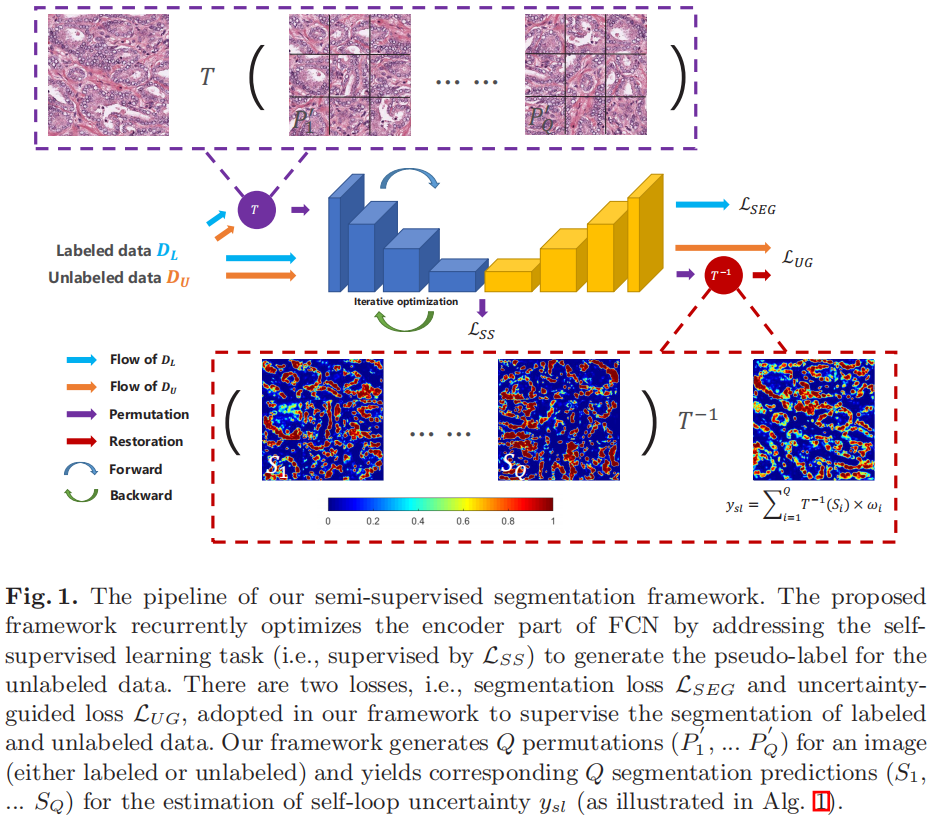
提出的自环不确定性是通过对具有自监督子任务(例如拼图)的完全卷积网络(FCN)的编码器进行循环优化而生成的。
训练集包含标注数据\(D_L\)和无标注数据\(D_U\),提出的方法包含三个loss(\(L_{SEG}, L_{UG}, L_{SS}\)),\(L_{SEG}\)用户有标注数据的分割训练,\(L_{SS}\)用户学习两个数据源的数据信息并生成自循环不确定性图,\(L_{UG}\)用于增强无标注数据的分割性能。

Self-supervised Sub-task
自监督损失\(L_{SS}\)旨在利用原始数据中包含的丰富信息并产生自环不确定性。
本文使用由平移和旋转变换组成的拼图作为自我监督的子任务来反复优化FCN的编码器并产生自环不确定性。例如将图像切分为\(3 \times 3\)的拼图,然后进行排序。进行K次排序组合,选择最大汉明距离图像放入排序池中\(P=(P_1, P_2, ..., P_{9!})\)。
每次迭代训练选取从\(K=100\)中选取\(Q \ll K, Q=10\)次,从中选取一个作为替代。同时,使用过K组图像对FCN的编码器进行更新,可以看做K个类别的分类任务。
Uncertainty-guided Loss
本文采用均方误差损失作为不确定性指导,\(y_{sl}\)为伪标签 \[ \mathcal{L}_{U G}\left(S_{x}, y_{s l}\right)=\frac{\sum_{H \times W} \mathbb{I}\left(y_{s l}>t h\right)\left\|S_{x}-y_{s l}\right\|^{2}}{\sum_{H \times W} \mathbb{I}\left(y_{s l}>t h\right)} \]
目标函数
\[ \mathcal{L}=\sum_{j=1}^{N} \mathcal{L}_{S E G}\left(x_{j}, y_{j}\right)+\sum_{j=N+1}^{N+M} \mathcal{L}_{U G}\left(x_{j}, y_{s l}\right)+\sum_{j=1}^{N+M} \sum_{i=1}^{Q} \mathcal{L}_{S S}\left(T_{P_{i}^{\prime}}\left(x_{j}\right), g_{i}\right) \]
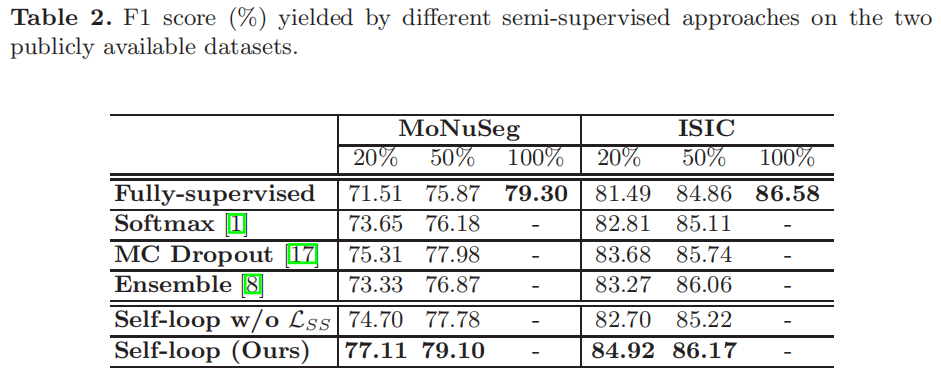
Experiments