Motivation
- 现有图像跨域翻译模型都有不错的性能来辅助图像分割任务,然而这些模型在翻译过程中不能很好保留图像的细节。
- CT与MRI之间的巨大差异,往往会导致性能不佳,在临床上重要性较低,而且成对的CT和MRI数据通常很难收集到。本文考虑CT图像的非增强图像与增强图像的转换问题。
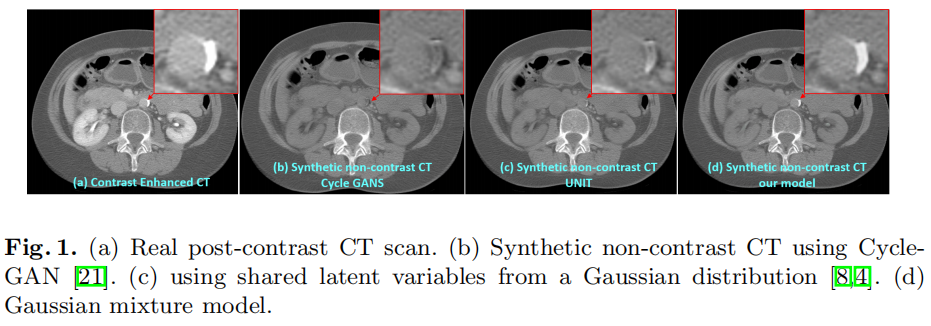
- 为了在医学图像转换过程中保留精细的结构,本文提出了一个基于patch的模型,该模型使用了来自高斯混合模型的共享潜在变量。
Methods
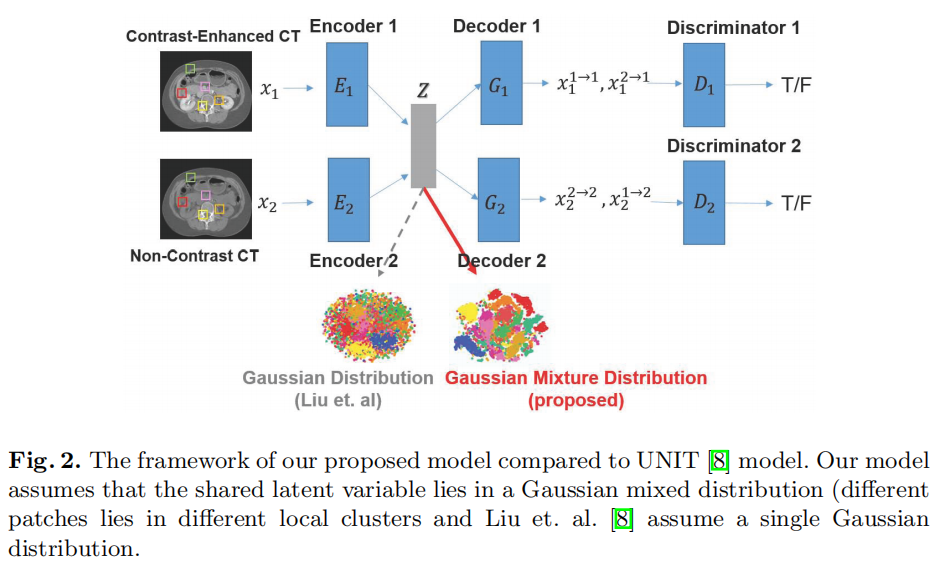
Unsupervised Image-to-Image Translation Networks (UNIT)
- 整体网络结构由两组变分自编码器组成分别用于两个不同的数据域,并通过共享的潜在空间\(Z\)实现图像翻译。
- 共享的潜在空间独立于源域和目标域,并被强制遵循具有unit variance的高斯分布。
Patch-Based Mixtures Gaussian Image-to-Image Translation
使用整张图像会导致细节丢失,本文提出基于Patch的方法,从源域和目标域随机选取相同位置的图像块进行实验。
两个编码器和两个生成器组成了两个VAE模型\(E_1(x_1, \theta_1), E_2(x_2, \theta_2)\),训练损失中加入了KL散度: \[ \begin{array}{l} \mathcal{L}_{V A E_{1}}\left(E_{1}, G_{1}, \boldsymbol{\Theta}_{1}, \mathbf{\Sigma}_{1}, \boldsymbol{\Sigma}_{z}, \mu_{z}\right)=\lambda_{1} \operatorname{KL}\left(q_{1}\left(z \mid x_{1}\right)|| p(z)\right) \\ -\lambda_{2} \mathbb{E}_{z \sim q_{1}\left(z \mid x_{1}\right)}\left[\log p G_{1}\left(x_{1} \mid z\right)\right] \\ \mathcal{L}_{V A E_{2}}\left(E_{2}, G_{2}, \boldsymbol{\Theta}_{2}, \boldsymbol{\Sigma}_{2}, \boldsymbol{\Sigma}_{z}, \mu_{z}\right)=\lambda_{1} \operatorname{KL}\left(q_{2}\left(z \mid x_{2}\right) \| p(z)\right) \\ -\lambda_{2} \mathbb{E}_{z \sim q_{2}\left(z \mid x_{2}\right)}\left[\log p G_{1}\left(x_{2} \mid z\right)\right] \end{array} \] 除此之外还有两个对抗生成网络\(GAN_1={G_1, D_1}, GAN_2={G_2, D_2}\)。如果分别从第一或第二域采样图像,则D1,D2被约束为输出true,如果分别从G1,G2生成图像,则D1,D2被约束为false。 \[ \begin{array}{l} \mathcal{L}_{G A N_{1}}\left(E_{2}, G_{1}, D_{1}, \boldsymbol{\Theta}_{1}, \mathbf{\Sigma}_{1}, \mathbf{\Sigma}_{z}, \mu_{z}\right)=\lambda_{0} \mathbb{E}_{x_{1} \sim P_{\mathcal{X}_{1}}}\left[\log D_{1}\left(x_{1}\right)\right] \\ +\lambda_{0} \mathbb{E}_{z \sim q_{2}\left(z \mid x_{2}\right)}\left[\log D_{1}\left(G_{1}(z)\right)\right] \\ \mathcal{L}_{G A N_{2}}\left(E_{1}, G_{2}, D_{2}, \Theta_{2}, \boldsymbol{\Sigma}_{2}, \boldsymbol{\Sigma}_{z}, \mu_{z}\right)=\lambda_{0} \mathbb{E}_{x_{2} \sim P_{\mathcal{X}_{2}}}\left[\log D_{2}\left(x_{2}\right)\right] \\ +\lambda_{0} \mathbb{E}_{z \sim q_{1}\left(z \mid x_{1}\right)}\left[\log D_{2}\left(G_{2}(z)\right)\right] \end{array} \] 还加入了循环一致性约束: \[ \begin{array}{l} \mathcal{L}_{C C_{2}}\left(E_{1}, G_{1}, E_{2}, G_{2}, \boldsymbol{\Theta}_{1}, \boldsymbol{\Theta}_{2}, \boldsymbol{\Sigma}_{1}, \boldsymbol{\Sigma}_{2}, \boldsymbol{\Sigma}_{z}, \mu_{z}\right) \\ =\lambda_{3} \operatorname{KL}\left(q_{1}\left(z \mid x_{1}\right) \| p(z)\right) \\ +\lambda_{4} \operatorname{KL}\left(q_{2}\left(z \mid x_{1}^{1->2}\right) \| p(z)\right)-\lambda_{4} \mathbb{E}_{z \sim q_{2}\left(z \mid x_{1}^{1}>2\right)}\left[\log p G_{1}\left(x_{1} \mid z\right)\right] \\ \mathcal{L}_{C C_{2}}\left(E_{2}, G_{2}, E_{1}, G_{1}, \boldsymbol{\Theta}_{1}, \boldsymbol{\Theta}_{2}, \boldsymbol{\Sigma}_{1}, \boldsymbol{\Sigma}_{2}, \boldsymbol{\Sigma}_{z}, \mu_{z}\right) \\ =\lambda_{3} \operatorname{KL}\left(q_{2}\left(z \mid x_{2}\right) \| p(z)\right) \\ +\lambda_{4} \operatorname{KL}\left(q_{1}\left(z \mid x_{2}^{2->1}\right) \| p(z)\right)-\lambda_{4} \mathbb{E}_{z \sim q_{1}\left(z \mid x_{2}^{2}>1\right)}\left[\log p G_{2}\left(x_{2} \mid z\right)\right] \end{array} \] 最终损失为: \[ \begin{array}{l} \arg \min \left(E_{1}, E_{2}, G_{1}, G_{2}, \Theta_{1}, \Theta_{2}, \boldsymbol{\Sigma}_{1}, \boldsymbol{\Sigma}_{2}, \boldsymbol{\Sigma}_{z}, \mu_{z}\right) \max \left(D_{1}, D_{2}\right) \\ \mathcal{L}_{V A E_{1}}\left(E_{1}, G_{1}, \boldsymbol{\Theta}_{1}, \boldsymbol{\Sigma}_{1}, \boldsymbol{\Sigma}_{z}, \mu_{z}\right)+\mathcal{L}_{V A E_{2}}\left(E_{2}, G_{2}, \boldsymbol{\Theta}_{1}, \boldsymbol{\Sigma}_{1}, \boldsymbol{\Sigma}_{z}, \mu_{z}\right) \\ +\mathcal{L}_{C C 1}\left(E_{1}, G_{1}, E_{2}, G_{2}, \boldsymbol{\Theta}_{1}, \boldsymbol{\Sigma}_{1}, \boldsymbol{\Theta}_{2}, \boldsymbol{\Sigma}_{2}, \boldsymbol{\Sigma}_{z}, \mu_{z}\right) \\ +\mathcal{L}_{C C 2}\left(E_{1}, G_{1}, E_{2}, G_{2}, \boldsymbol{\Theta}_{1}, \boldsymbol{\Sigma}_{1}, \boldsymbol{\Theta}_{2}, \boldsymbol{\Sigma}_{2}, \boldsymbol{\Sigma}_{z}, \mu_{z}\right) \\ +\mathcal{L}_{G A N_{1}}\left(E_{1}, G_{1}, D_{1}, \boldsymbol{\Theta}_{1}, \boldsymbol{\Sigma}_{1}\right)+\mathcal{L}_{G A N_{2}}\left(E_{2}, G_{2}, D_{2}, \Theta_{2}, \boldsymbol{\Sigma}_{2}\right) \end{array} \]
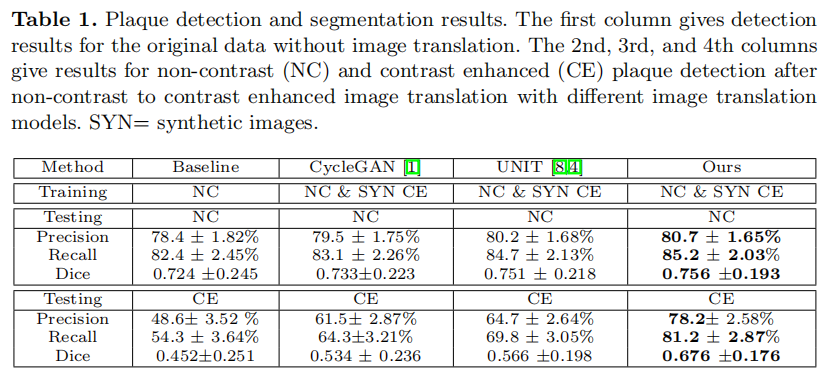
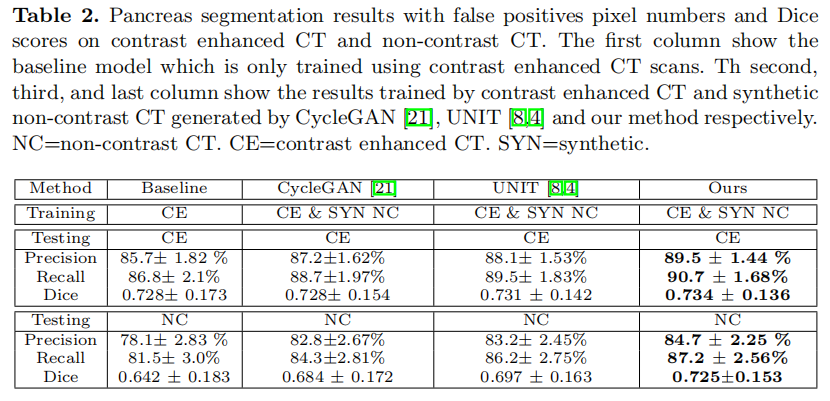
Experiments