图卷积之前了解不多,这篇文章没怎么读懂,还是做一下记录。
Motivation
现有方法通常依赖于位置信息和对冠状动脉树的拓扑结构的先验知识,当主分支混乱时,很容易产生不好的结果。
目前图卷积在结构数据中应用广泛,这篇文章基于GCN提出了conditional partial-residual graph convolutional network (CPR-GCN)。
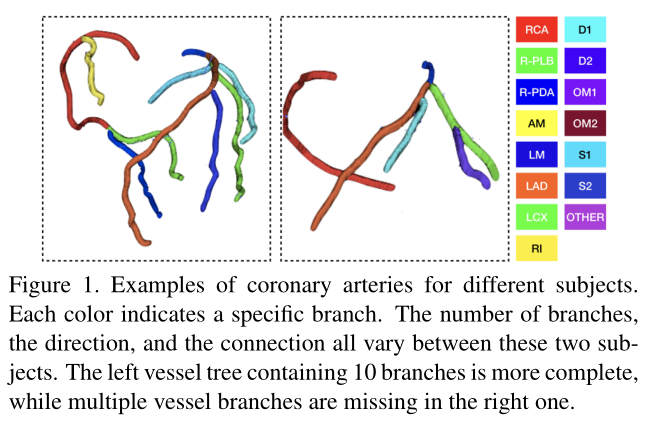
如下图,受试者之间的冠状动脉相差很大,这是标记系统的主要挑战。
本文贡献:
- 提出了CPR-GCN,这是一种条件的残差图卷积网络,可以端到端标记冠状动脉树。
- 本文首次提出在冠状动脉标注领域中使用3D图像特征。
- CPR-GCN与混合模型(3D CNN结合BiLSTMs)联合训练,有很好的效果。
相关工作中提出的问题:
- TreeLab-Net主要是基于两个分支的网络,而在冠状动脉中经常有多个分支,这个超出了TreeLab-Net的能力。
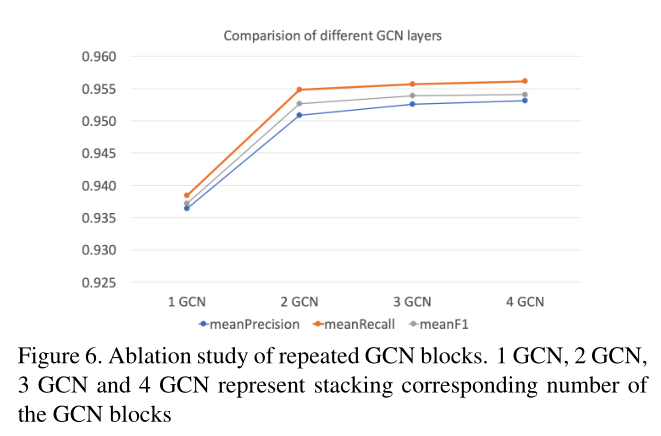
- 堆叠多个GCN层容易出现过渡平滑。
Methods
CPR-GCN主要包含partial-residual GCN和conditions extractor两部分。
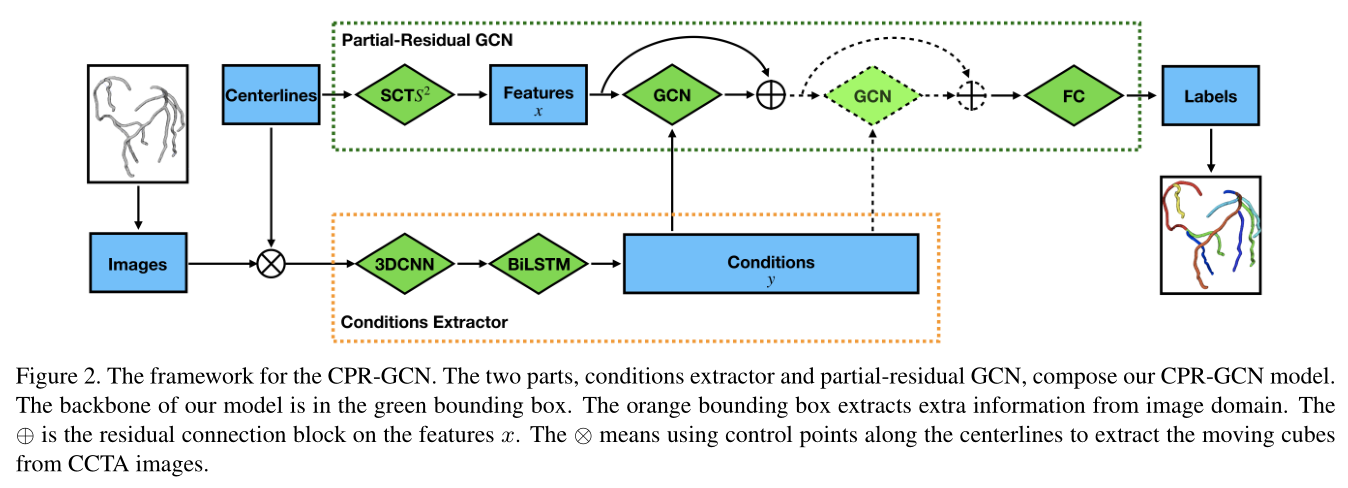
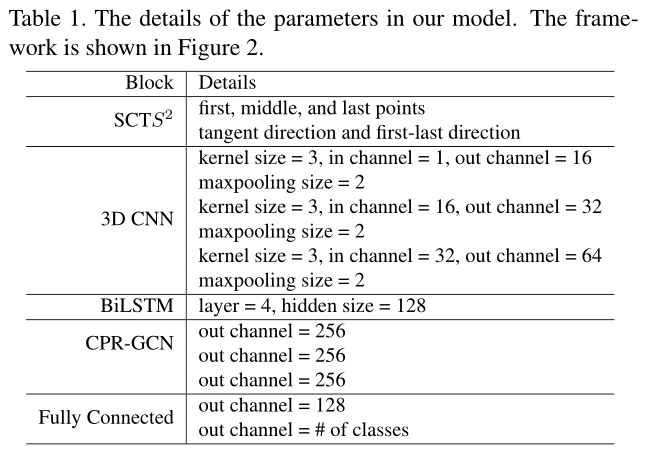
Position Domain Features
参考文献【22】中使用球状坐标转换将3D坐标\(P_k=[(x_i, y_i, z_i)]_{i=1}^{Length_k}\)转换成了2D坐标\([(\varphi_i, \theta_i)]_{i=1}^{Length_k}\)。
角度范围在\([0,2\pi)\),容易在\(2\pi\)与\(0\)之间出现问题。
本文使用\(S^2\)形式表示\(\varphi , \theta\)克服此问题。
这里使用\(2 \times 2\)的矩阵\(M=\left[\begin{array}{ll}\sin \theta & \sin \varphi \\ \cos \theta & \cos \varphi\end{array}\right]\),\(\sin(\cdot), \cos(\cdot)\)的周期使得\(M\)在整个\(S^2\)上是稳定的,这种坐标变换被称为\(SCT S^2\)。
\[\begin{array}{ll} x=r \sin \theta \cos \varphi & r=\sqrt{x^{2}+y^{2}+z^{2}} \\ y=r \sin \theta \sin \varphi & \cos \theta=z / r, \theta \in[0, \pi] \\ z=r \cos \theta & \sin \varphi=x /(\operatorname{rin} \theta), \cos \varphi=y /(\operatorname{rin} \theta) \end{array}\]
Image Domain Conditions
大多数医学图像(MRI、CCTA)属于3D信息,具有顺序的依赖性,这里使用3D CNN提取空间特征,然后使用BiLSTM学习顺序特征。
将最后一个状态作为条件信息,因为图像的重要性不如位置域特征。
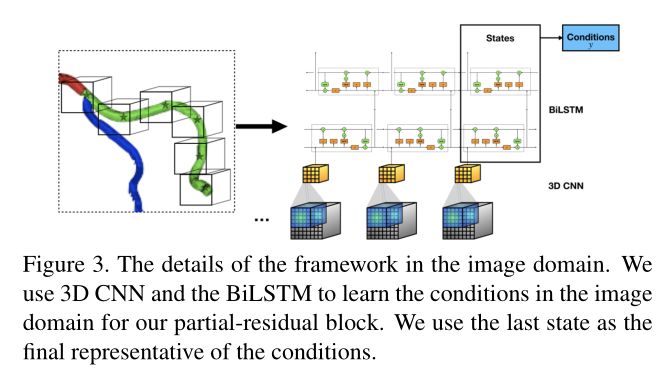
Partial-Residual Block of GCN
图卷积的计算公式如下所示:
\[\begin{array}{l} H^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{l} W^{l}\right) \\ \tilde{A}=A+I_{N}, \tilde{D}_{i i}=\sum_{j} \tilde{A}_{i j} \end{array}\]
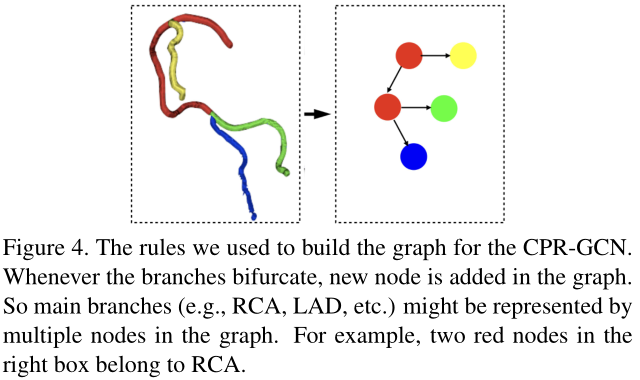
将来自位置特征\(x\)与CCTA图像域条件\(y\)的组合作为图模型中的节点,边缘定义为parent-children关系。
每当分支结构存在下级分支时,再加入更多节点。
Experiments