Code: https://github.com/facebookresearch/mixup-cifar10
Motivation
在大多数成功的案例中,网络模型有两处共同点:
- 训练神经网络主要依靠经验风险最小化(ERM)
- 网络的规模和数据集规模成正比
ERM收敛的重要保证是模型规模不随数据集规模增加而增加。然而目前的模型大多随着数据集规模发生变化,网络只是单纯“记住了”这些数据。
Methods
机器学习的目标是为了期望风险最小化:
\[ R(f)=\int \ell(f(x), y) \mathrm{d} P(x, y) \]
其中\(\ell\)表示损失函数。实际问题中,\(P\)的分布是未知的,通常使用经验分布来近似表示: \[ P_{\delta}(x, y)=\frac{1}{n} \sum_{i=1}^{n} \delta\left(x=x_{i}, y=y_{i}\right) \] 由此得到: \[ R_{\delta}(f)=\int \ell(f(x), y) \mathrm{d} P_{\delta}(x, y)=\frac{1}{n} \sum_{i=1}^{n} \ell\left(f\left(x_{i}\right), y_{i}\right) \] 经验风险最小化虽然可以计算效率很高,但经验风险只关注有限的n个样例。当数据超出训练样例范围时,可能会出现一些不可知的错误。
本文提出一种通用的邻域分布,称为mixup: \[ \mu\left(\tilde{x}, \tilde{y} \mid x_{i}, y_{i}\right)=\frac{1}{n} \sum_{j}^{n} \underset{\lambda}{\mathbb{E}}\left[\delta\left(\tilde{x}=\lambda \cdot x_{i}+(1-\lambda) \cdot x_{j}, \tilde{y}=\lambda \cdot y_{i}+(1-\lambda) \cdot y_{j}\right)\right] \] 其数据为直接将x和y进行混合: \[ \tilde{x}=\lambda x_i+(1-\lambda)x_j \]
\[ \tilde{y} = \lambda y_i + (1-\lambda) y_i \]

mixup实现方式非常直观,实现过程中有考虑以下几点:
- 将三个或三个以上融合,效果几乎和两个一样,而且增加了mixup的时间
- 将mixup应用于单个loader,对同一个minibatch中的数据进行混合,这样的策略和整个数据集随机打乱的效果是一样的,还能减少IO的开销
- 相同标签的数据进行mixup作用不大
mixup的作用:
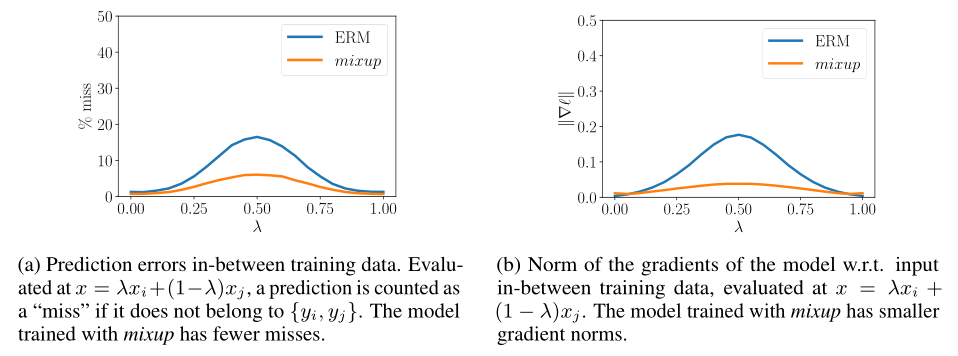
mixup可以理解为一种数据增强形式,告诉训练器尽可能训练出线性的边界。这样能减少过拟合,而且线性模型最简单,符合奥卡姆剃刀。
Experiments
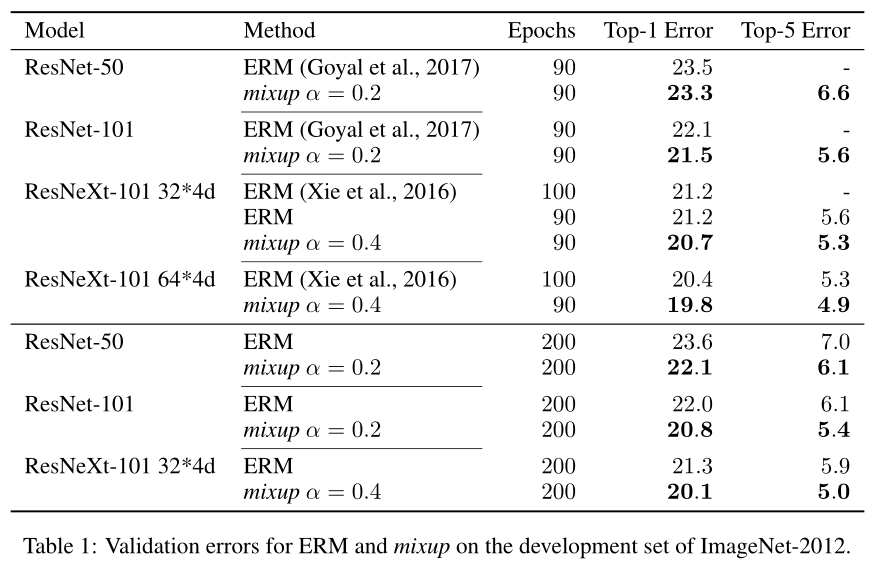
ImageNet 分类
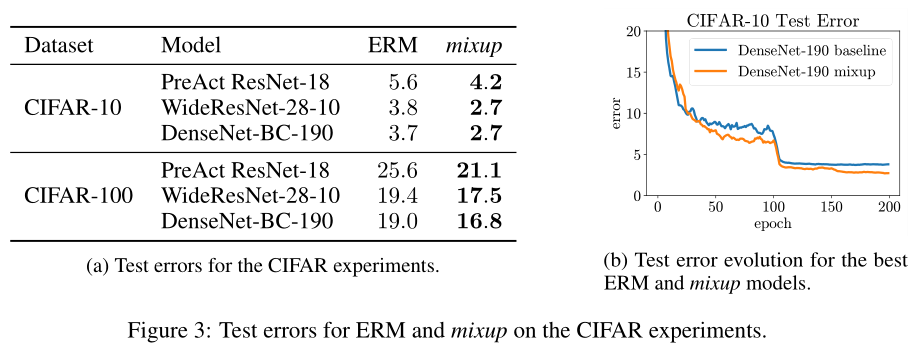
CIFAR-10 与 CIFAR-100
语音数据

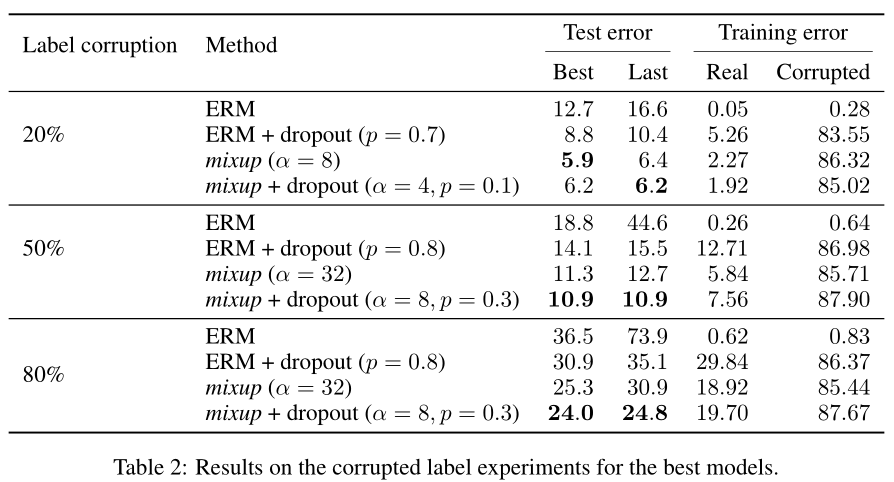
Memorization of corrupted labels
Robustness to Adversarial Expamples
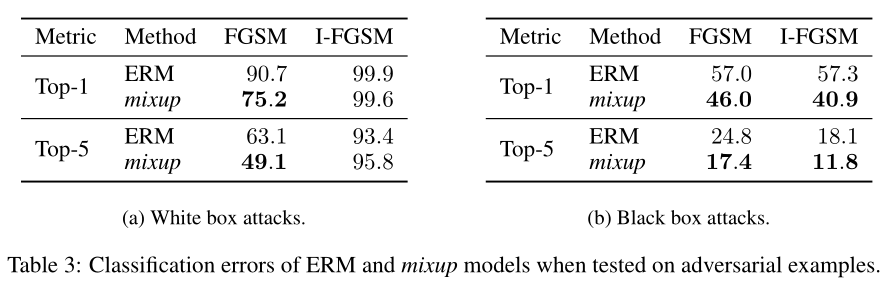
Tabular Data
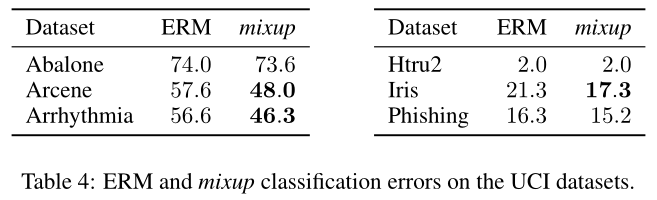
Stabilization of Generative Adversarial Networks
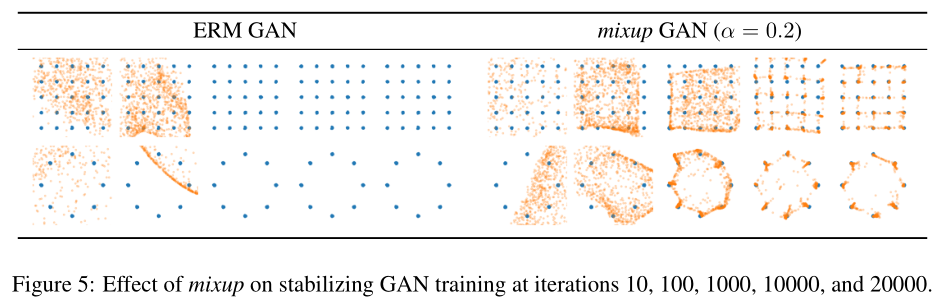
Ablation Studies
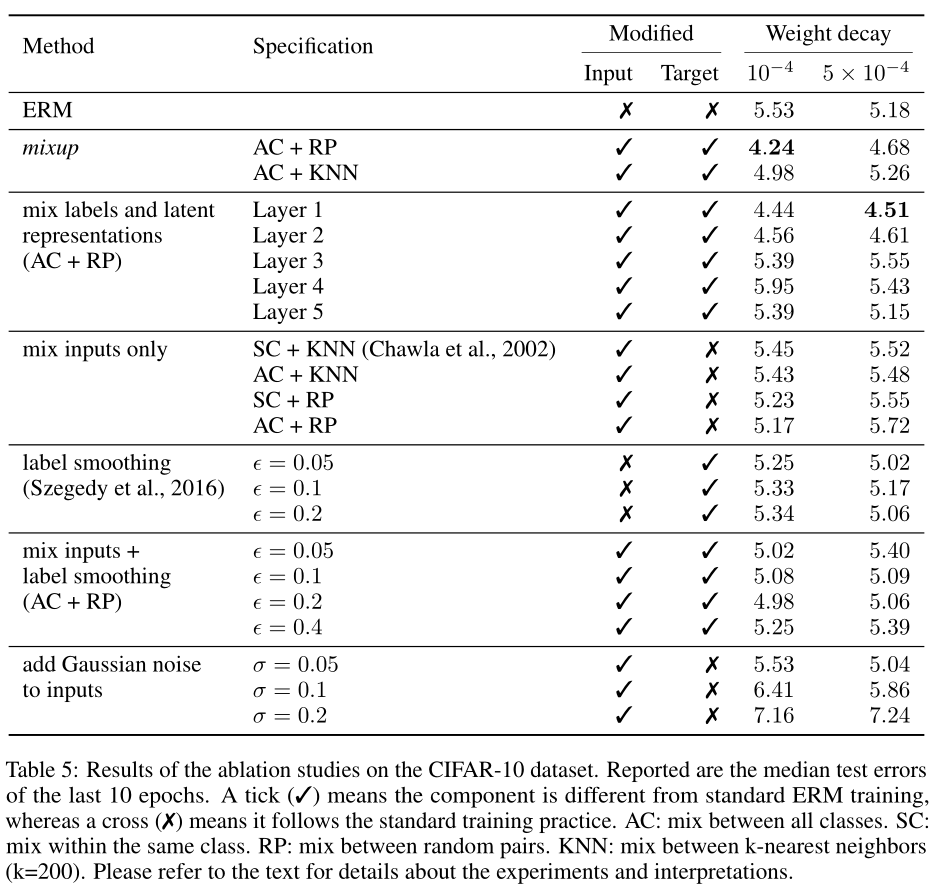
Discussion
- 还没有一个很好的理论来理解这种偏差-方差折中的“最佳点”
- 作者通过实验推测,增加模型容量将使训练误差对大的\(\alpha\)的敏感度降低,因此mixup的优势将更加明显
- 是否有可能使类似的想法适用于其他类型的监督学习问题,例如回归和结构化预测?尽管讲mixup泛化到回归问题很简单,但应用于结构化预测问题(如图像分割)的问题还不是很明显
- 类似的方法在监督学习之外可以用吗?插值原理是合理的归纳偏差,也可能有助于无监督、半监督和强化学习。
- 是否能够将mixup拓展到特征-标签之外来保证远离训练数据时模型的健壮性?