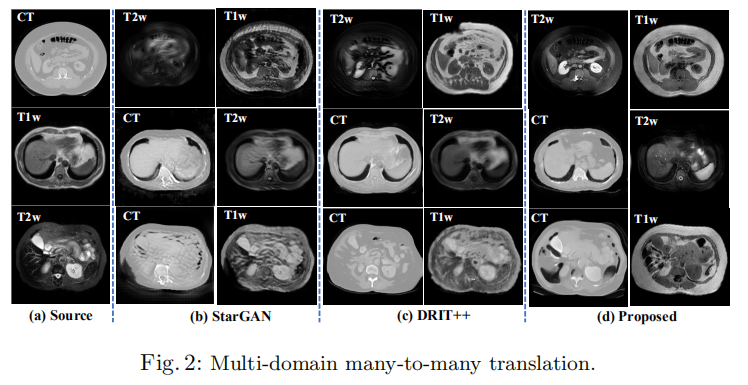
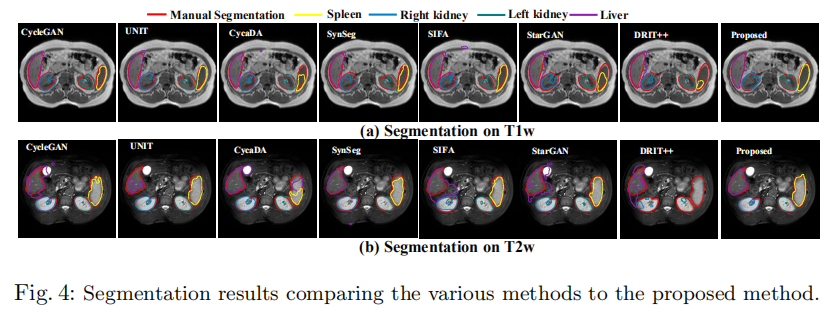
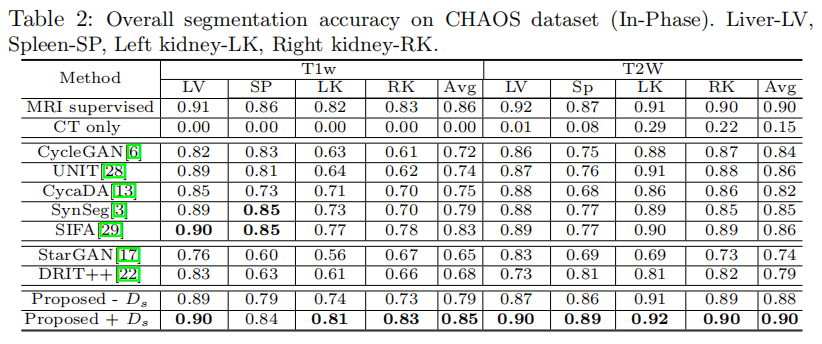
Motivation
本文方法使用变分自编码器(VAE)将图像内容与样式分开。
- VAE约束样式特征编码以匹配通用(高斯)先验,该先验加总后可以覆盖所有源域和目标域的样式
- 提取的图像样式被转换为潜在样式缩放代码,该代码将生成器可以根据目标域图像内容特征的代码生成多模态图像
- 介绍了一种联合分布匹配判别器,能够将翻译后的图像与任务相关的分割概率图相结合,以进一步约束和规范化图像到图像(I2I)的翻译
Methods
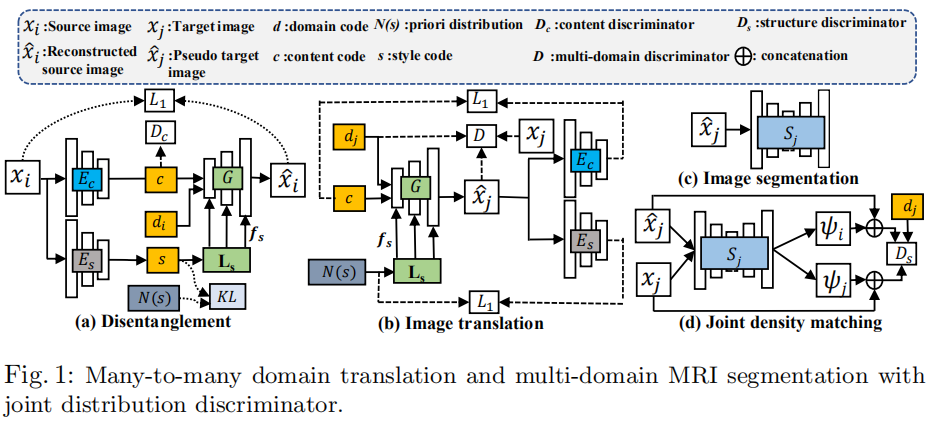
Feature disentanglement and image translation
本文主要使用VAE将图像的内容和样式进行分离。假设所有域的潜在样式分布为高斯分布,Encoder \(E_s\)使用KL散度提取与此先验匹配的样式代码。样式代码之后通过latent scale (LS)层转换为潜在风格\(f_s\)。域代码是通过与内容代码按通道进行级联注入的。
VAE中,自我重建损失与KL散度损失合并为: \[ L_{V A E}=\sum_{i} E_{x_{i} \sim X_{i}}\left[D_{K L}\left(E_{s}\left(x_{i}\right) \| z\right)\right]+\left\|\hat{x}_{i}-x_{i}\right\|_{1} \] 领域不变内容特征是通过对抗训练由: \[ L_{a d v}^{c}=\sum_{i} \sum_{j ; j \neq i} \underset{x_{i} \sim X_{i} \atop {x_j \sim X_j}}{\mathbb{E}}\left[\log \left(D_{c}\left(E_{c}\left(x_{i}\right)\right)\right)\right]+\mathbb{E}\left[1-\log \left(D_{c}\left(E_{c}\left(x_{j}\right)\right)\right)\right] \] Content reconstruction loss: \[ L_{c}=\sum_{i} \sum_{j ; j \neq i} \underset{x_{i} \sim X_{i} \atop {x_j \sim X_j}}{\mathbb{E}}\left|\left| E_c(x_i)-E_c(\hat{x}_j ) \right|\right| \] Latent code regression loss \[ L_{l r}=\sum_{i} \sum_{j ; j \neq i} \underset{x \sim X_{i}}{\mathbb{E}}\left\|z-E_{s}\left(G\left(E_{c}(x), L_{s}(z), d_{j}\right)\right)\right\|_{1} \] Domain adversarial loss \[ \begin{aligned} \min _{G} \max _{D} L_{G A N}=& \sum_{i} \sum_{j ; j \neq i}\left\{\underset{x_{j} \sim X_{j}}{\mathbb{E}}\left[\log \left(D\left(x_{j}, d_{j}\right)\right)\right]+\right.\\ & \underset{x_{i} \sim X_{i}}{\mathbb{E}}\left[\frac{1}{2} \log \left(1-D\left(G\left(E_{c}\left(x_{i}\right), L_{s}\left(E_{s}\left(x_{j}\right)\right), d_{j}\right), d_{j}\right)\right)\right]+\\ & \underset{z \sim N(0,1)}{\mathbb{E}}\left[\frac{1}{2} \log \left(1-D\left(G\left(E_{c}\left(x_{i}\right), L_{s}(z), d_{j}\right), d_{j}\right)\right)\right\} \end{aligned} \] Mode seeking loss \[ L_{m s}=\max _{G}\left(\sum_{i} \sum_{j ; j \neq i} \frac{d_{I}\left(G\left(E_{c}\left(x_{i}\right), L_{s}\left(z_{1}\right), d_{j}\right), G\left(E_{c}\left(x_{i}\right), L_{s}\left(z_{2}\right), d_{j}\right)\right)}{d_{z}\left(z_{1}, z_{2}\right)}\right) \]
Segmentation
\[ L_{s e g}=\sum_{j, j \neq i} \underset{\hat{x}_{j} \sim \hat{X}_{j}, l_{i} \sim Y_{i}}{\mathbb{E}}\left[\log P\left(l_{i} \mid S_{j}\left(\hat{x}_{j}\right)\right)\right] \]
Joint distribution structure discriminator \[ L_{s t}=\sum_{j ; j \neq i}\left\{\mathbb{E}_{x_{j} \sim X_{j}}\left[\log \left(D_{s}\left(x_{j}, \psi_{j}, d_{j}\right)\right)\right]+\mathbb{E}_{\hat{x}_{j} \approx X_{j}}\left[\log \left(1-D_{s}\left(\hat{x}_{j}, \hat{\psi}_{j}, d_{j}\right)\right)\right]\right\} \] Total Loss \[ L_{\text {total}}=L_{G A N}+\lambda_{\text {vae}} L_{V A E}+\lambda_{c} L_{\text {adv}}^{c}+\lambda_{\text {lr}} L_{l r}+\lambda_{\text {ms}} L_{m s}+\lambda_{\text {st}} L_{s t}+\lambda_{\text {seg}} L_{\text {seg}} \]
Experiments