Motivation
- 准确的多器官腹部CT分割对于许多临床应用是必不可少的
- 通常数据集倍部分标注,如胰腺数据集仅标注胰腺儿其他部分标记为背景
- 背景标签通常包含其他感兴趣器官,在多器官分割中容易引起误导
3D可视化几个腹部器官,可以看出患者的腹部器官大小分布很相似。
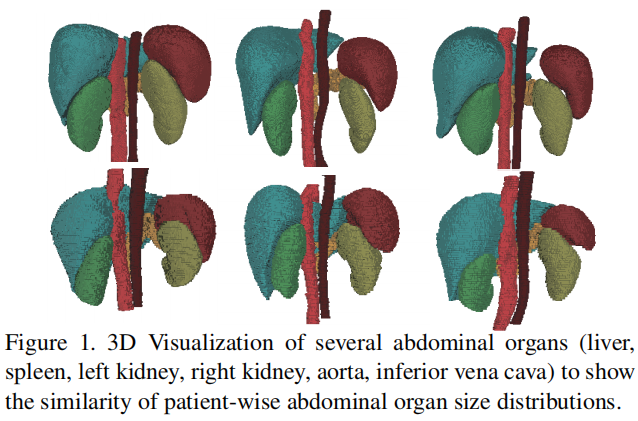
Methods
将腹部器官大小的解剖学先验结合起来,假设腹部的平均器官大小分布应该接近它们的经验分布,从完全标记的数据集获得的先前统计数据。
通过先验感知损失来实现,先验损失作为辅助和软约束,将不同器官的平均输出大小分布应近似于先前的比例。
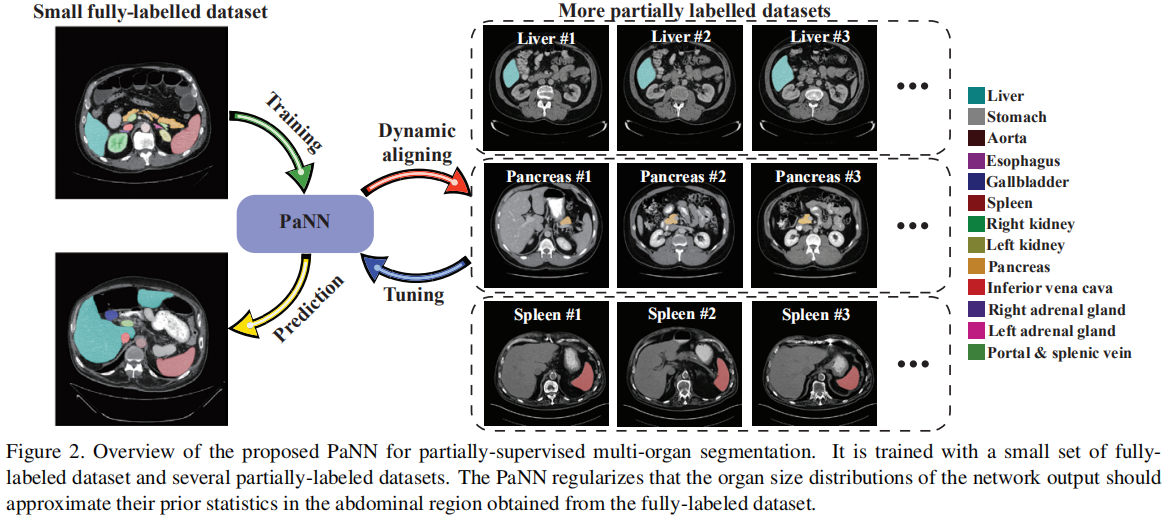
Partial Supervision
假设医学图像分析中常见的数据集有以下特征:
- 数据标准化,扫描数据的内部结构是一致的
- 内部器官具有解剖和空间关系,如胃、十二指肠、小肠和结肠以固定顺序连接。
一个简单的解决方案是直接在完全标注和部分标注数据上交替训练分割模型。然而这种类似EM的方法需要高质量的伪标签,且无法引入准确的解剖学先验。
本文提出PaNN模型,嵌入解剖学先验,将其作为附加惩罚项,充当软约束使得器官大小的平均分布应接近经验比例。通过计算完全标记数据集的器官大小统计信息获得此先验。
Prior-aware Loss
定义全标注数据的标签分布为\(q \in \R^{(|\mathcal{L}|+1)\times 1}\),部分标注的网络输出为\(p\),则部分标注数据的分布为\(\overline{p}=\frac{1}{N}\sum_{t=1}^{T}{\sum_{i\in P_t}{\sum_{j}{p_{ij}}}}\)。
通过KL散度匹配两个数据的分布,先验损失定义为: \[ \mathcal{J}_c = KL(q|\overline{p}) = H(q, \overline{p}) - H(q) = qlog{\overline{p}} + (1-q)log{(1-\overline{p})} + const \] 等式的基本原理是不同器官的大小分布p赢近似于它们的经验比例q,通常反映了特定领域知识。
最终的训练目标为: \[ \min _{\boldsymbol{\Theta}, \mathbf{Y}_{\mathrm{P}}} \mathcal{J}_{\mathrm{L}}(\boldsymbol{\Theta})+\lambda_{1} \mathcal{J}_{\mathrm{P}}\left(\boldsymbol{\Theta}, \mathbf{Y}_{\mathrm{P}}\right)-\lambda_{2} \mathcal{J}_{\mathrm{C}}(\boldsymbol{\Theta}) \] 前两项分别为在全标注数据和部分标注数据上的交叉熵损失,最后一项作为软约束来稳定训练过程。 \[ \mathcal{J}_{\mathrm{L}}=-\frac{1}{N} \sum_{i \in \mathrm{L}} \sum_{j} \sum_{l=0}^{|\mathcal{L}|} \mathbb{1}\left(y_{i j}=l\right) \log p_{i j}^{l} \]
\[ \begin{array}{r} \mathcal{J}_{\mathrm{P}}=-\frac{1}{N} \sum_{t=1}^{T} \sum_{i \in \mathrm{P}_{t}} \sum_{j} \sum_{l=0}^{|\mathcal{L}|}\left\{\mathbb{1}\left(y_{i j}=l\right) \log p_{i j}^{l}\right. \\ \left.+\mathbb{1}\left(y_{i j}^{\prime}=l\right) \log p_{i j}^{l}\right\} \end{array} \]
Derivation
将\(\mathcal{J}_C\)展开得到: \[ \begin{aligned} \mathcal{J}_{\mathrm{C}}=& \sum_{l=0}^{|\mathcal{L}|}\left\{q^{l} \log \frac{1}{N} \sum_{t=1}^{T} \sum_{i \in \mathrm{P}_{t}} \sum_{j} p_{i j}^{l}+\right.\\ &\left.\left(1-q^{l}\right) \log \left(1-\frac{1}{N} \sum_{t=1}^{T} \sum_{i \in \mathrm{P}_{t}} \sum_{j} p_{i j}^{l}\right)\right\}+\text {const} \end{aligned} \] 等式引入了器官尺寸分布\(\overline{p}\)的对数损失,和标准机器学习损失有很大不同,其他的是平均项在对数损失外部。通过随机梯度下降直接最小化损失项非常困难,随机梯度存在固有的偏差。
针对此问题,提出了随机的原始对偶梯度优化KL散度项。通过从对数损失中减去样本平均值,将先验损失转化为等效的min-max问题。引入两个辅助变量: \[ -\log \alpha=\max _{\beta}(\alpha \beta+1+\log (-\beta)) \] 定义\(\mathcal{v}\in \R^{|\mathcal{L}|\times 1}\)和\(\mu\in \R^{|\mathcal{L}|\times 1}\)为\(\overline{p}\)和\((1-\overline{p})\)的对偶变量: \[ \begin{aligned} -\log \bar{p}^{l} &=\max _{\nu^{l}}\left(\bar{p}^{l} \nu^{l}+1+\log \left(-\nu^{l}\right)\right) \\ -\log \left(1-\bar{p}^{l}\right) &=\max _{\mu^{l}}\left(\left(1-\bar{p}^{l}\right) \mu^{l}+1+\log \left(-\mu^{l}\right)\right) \end{aligned} \] 替换原始公式后得到对偶损失 \[ \begin{array}{c} \min _{\boldsymbol{\Theta}} \max _{\nu, \boldsymbol{\mu}} \sum_{l} q^{l}\left(\bar{p}^{l} \nu^{l}+1+\log \left(-\nu^{l}\right)\right) \\ \quad+\sum_{l}\left(1-q^{l}\right)\left(\left(1-\bar{p}^{l}\right) \mu^{l}+1+\log \left(-\mu^{l}\right)\right) \\ \Leftrightarrow \min _{\boldsymbol{\Theta}} \max _{\nu, \boldsymbol{\mu}} \sum_{l}\left(q^{l} \nu^{l}-\left(1-q^{l}\right) \mu^{l}\right) \bar{p}^{l}+q^{l} \log \left(-\nu^{l}\right) \\ \quad+\sum_{l}\left(1-q^{l}\right)\left(\mu^{l}+\log \left(-\mu^{l}\right)\right) \end{array} \] 这样样本的平均值从对数损失中取了出来,上述公式中省略了常数项。
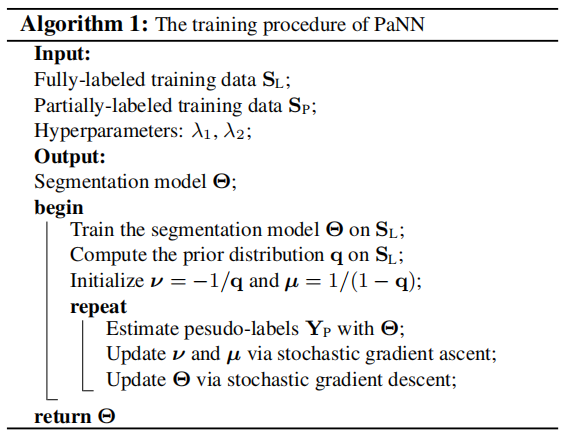
Model Training
训练分为两个阶段:
- 在全标注数据集上训练器官分割模型,目标是找到合适的初始化值\(\theta_O\),可以稳定第二阶段训练过程
- 在完全标注数据集和部分标注数据集的并集上训练模型,存在两组变量,网络权重和三个辅助变量\(\{ \mathcal{v}, \mu, Y_P \}\),交替训练优化
- 固定网络参数,更新辅助变量:首先估计伪标签\(Y_P\),同时优化另外两个辅助参数,通过随机梯度上升优化参数最大化问题。
- 固定辅助变量,更新网络:使用标准的随机梯度下降。
Experiments
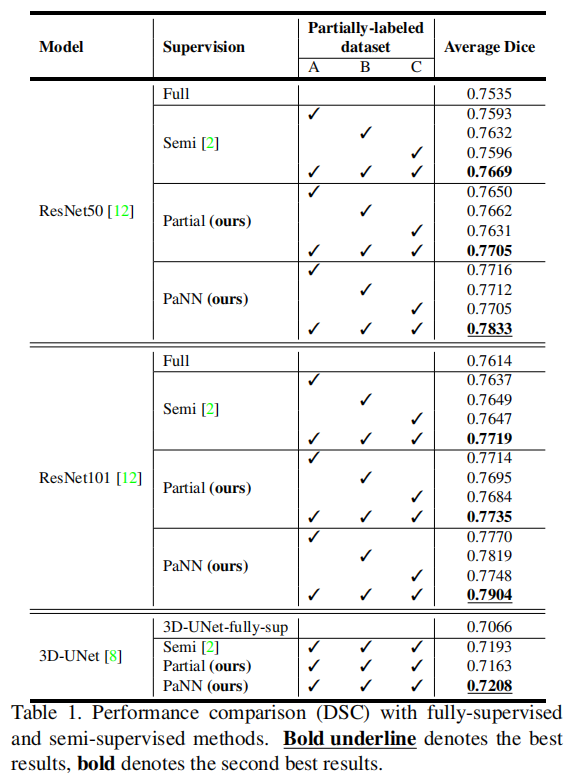
采用5折交叉验证,评价指标为Dice系数。