Code: https://github.com/googleinterns/wss
Pdf: https://arxiv.org/abs/2010.09713
Motivation
- 语义分割任务需要大量密集的标签,标注成本高
- 分割中结构化的输出应用在现有的半监督任务中存在特殊的困难(设计伪标签和数据增强)
本文提出PsudoSeg框架,利用图像级标签或无标签数据改善图像分割,贡献有三点:
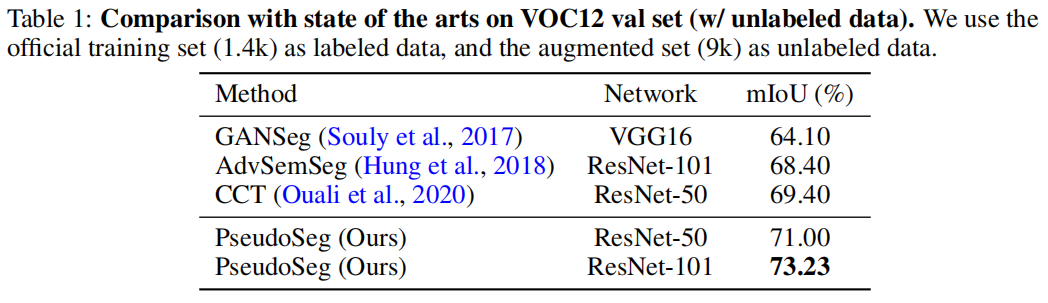
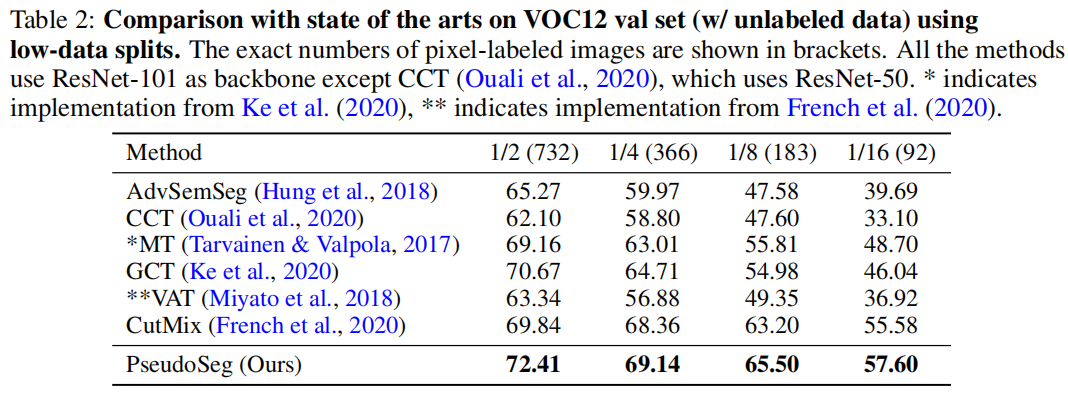
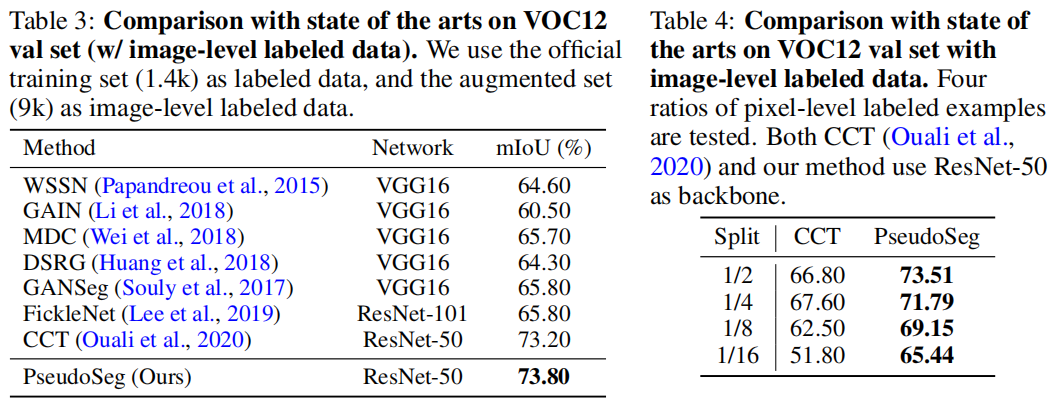
- 提出一个简单的单阶段框架,通过数量有限的像素标记数据和足够的未标记数据或图像级标记数据来改善语义分割。框架与网络结构无关。
- 直接应用在图像分类中验证的一致性训练方法会给分割带来特殊挑战。通过融合多源预测结果来获得较好的软伪标签以极大改善分割的一致性训练。
- 在多个数据集上进行实验,验证了方法的有效性。
Methods
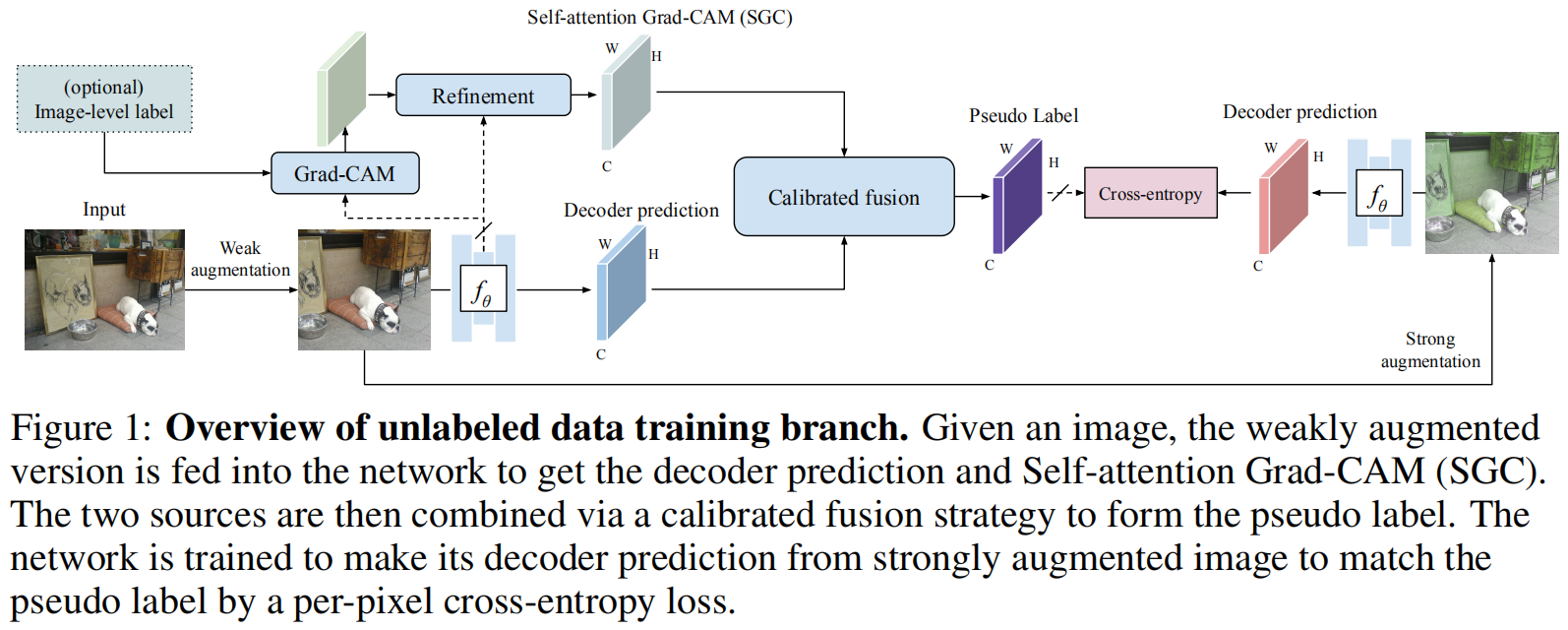
框架结构图如下:
问题定义
有监督损失为\(\mathcal{L}_s\)应用于有标注数据\(\mathcal{D}_l\),一致性损失\(\mathcal{L}_u\)应用于无标签数据\(\mathcal{D}_u\)。
\(\mathcal{L}_s\)为标准的cross-entropy loss: \[ \mathcal{L}_{\mathrm{s}}=\frac{1}{N \times\left|\mathcal{D}_{l}\right|} \sum_{x \in \mathcal{D}_{l}} \sum_{i=0}^{N-1} \text { Cross Entropy }\left(y_{i}, f_{\theta}\left(\omega\left(x_{i}\right)\right)\right) \] 一致性损失使用的提出的方法估计的伪标签\(\widetilde{y}\)进行训练 \[ \mathcal{L}_{\mathrm{u}}=\frac{1}{N \times\left|\mathcal{D}_{u}\right|} \sum_{x \in \mathcal{D}_{u}} \sum_{i=0}^{N-1} \text { CrossEntropy }\left(\widetilde{y}_{i}, f_{\theta}\left(\beta \circ \omega\left(x_{i}\right)\right)\right) \]
框架设计
如何生成想要的伪标签\(\widetilde{y}\)?
最直接的想法是使用训练好的分割模型的decoder的输出作为伪标签。然而在少量数据下这样生成的硬/软标签以及其他输出的后处理的结果都很差。
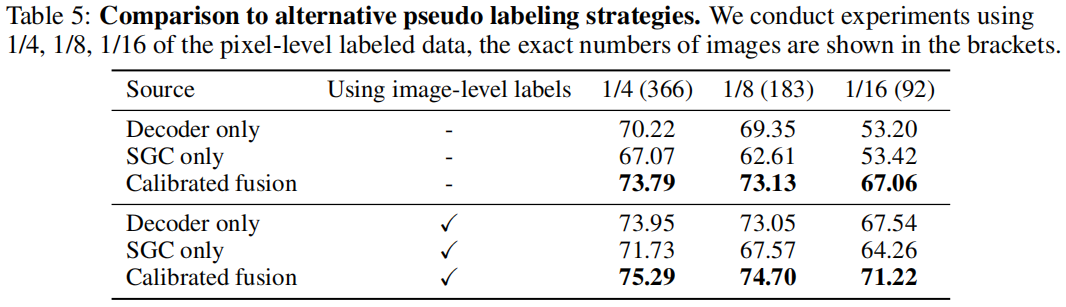
针对上述问题,本文方法有两个关键点:
- 寻求一种独特而有效的决策机制来补偿decoder输出的潜在错误。
- 融合多源预测结果生成一个较好的伪标签。
开始定位
与分割任务相比,定位任务相对简单,首先从定位角度提升decoder的预测结果。
CAM广泛应用于弱监督定位任务,本文采用Grad-CAM的一个变体进行定位。
从定位到分割
尽管CAM仅仅定位感兴趣的部分区域,但如果知道区域之间成对的相似性,可以将CAM分数从判别区域传播到其他未关注区域,可以利用这个特点实现从定位到分割的转换。本文中发现相似性度量方法Hypercolumn在这里很有效。
给定所有C个类别的Grad-CAM输出,将其看做spatially-flatten 2-D向量\(m \in \mathbb{R}^{L \times C}\),每一行\(m_i\)是区域\(i\)的每个类别的对应权重。使用核函数\(\mathcal{K}(·,·): \mathbb{R}^H \times \mathbb{R}^H \rightarrow \mathbb{R}\)测量给定特征的逐像素相似性。可以如下计算传播分数\(\hat{m_i} \in \mathbb{R}^C\): \[ \hat{m}_{i}=\left(m_{i}+\sum_{j=0}^{L-1} \frac{e^{\mathcal{K}\left(W_{k} h_{i}, W_{v} h_{j}\right)}}{\sum_{k=0}^{L-1} e^{\mathcal{K}\left(W_{k} h_{i}, W_{v} h_{k}\right)}} m_{j}\right) \cdot W_{c} \] 这个函数用于训练模型,使得m中的高值传播到特征空间的相邻区域,其中\(m_i\)为skip-connection。公式可以用自监督的乘法实现,最终得到self-attention Grad-CAM(SGC) maps。
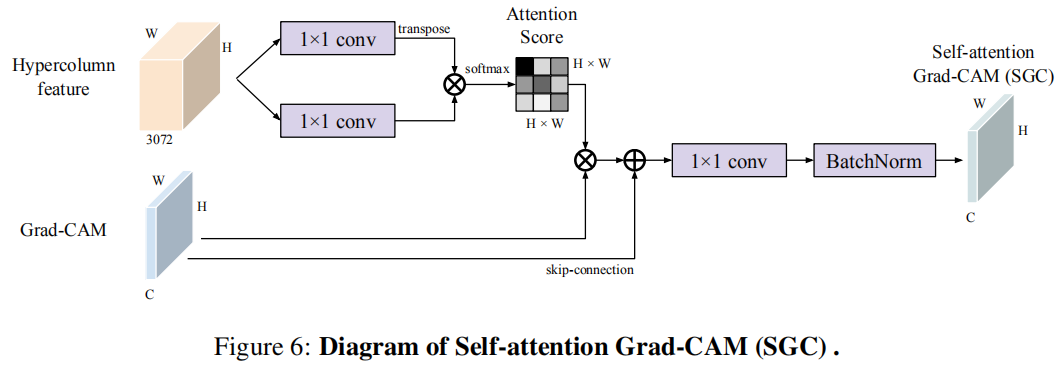
预测结果的融合
SGC图从低分辨率缩放到需要的大小,不能够很好输出清晰的边界,但与分割的decoder相比,能够更好生成的局部一致的分割图。
通过下面公式将SGC图和decoder的结果融合: \[ \mathcal{F}(\hat{p}, \hat{m})=\operatorname{Sharpen}\left(\gamma \operatorname{Softmax}\left(\frac{\hat{p}}{\operatorname{Norm}(\hat{p}, \hat{m})}\right)+(1-\gamma) \operatorname{Softmax}\left(\frac{\hat{m}}{\operatorname{Norm}(\hat{p}, \hat{m})}\right), T\right) \] 融合结果的成功来自两点:
- \(\hat{p}\)和\(\hat{m}\)来自不同决策机制,拥有不同程度的置信度。
- 分布的sharpening操作\(Sharpen(a, T)_i = \frac{a_i^{\frac{1}{T}}}{\sum_{j}^{C}{a_i^{\frac{1}{T}}}}\)
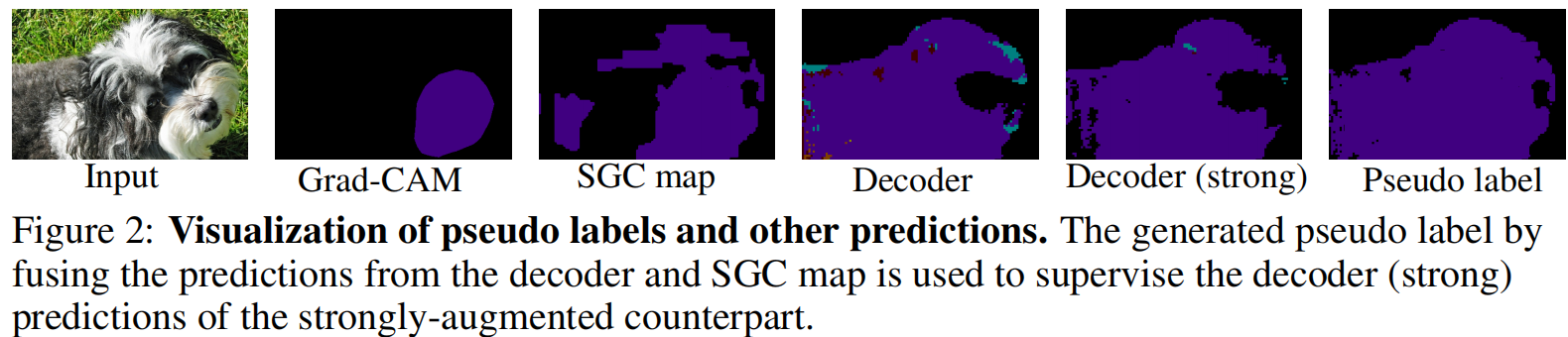
下图为不同阶段结果:
训练
最终的训练目标有两个额外的损失:分类损失\(\mathcal{L}_x\)和分割损失\(\mathcal{L}_{sa}\)。
首先,计算Grad-CAM时,在分割backbone后加一层分类头以及一个多标签的分类损失\(\mathcal{L}_x\)。
其次,SGC图使用一层卷积进行缩放,预测SGC图需要完全标注数据,使用到额外的分割损失\(\mathcal{L}_{sa}\)。
强数据增强使用到了color jittering,去除了所有形态学操作。此外还用到了随机CutOut操作进行结果提升。
Experiments